A cross section of an object in 3D is naturally 2D. This is an example of taking a 'slice' from a higher space to get an image in a space of lower dimension. We can slice any function like this. When we use 4D noise to make an animated 3D texture, the individual frames use a 3D slice of the 4D noise with the fourth (time) value held constant.

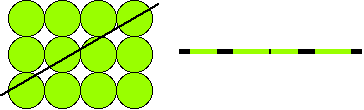
In this figure a 1D slice is taken from a 2D space. As the line cuts the circles they are represented by green extents. In a similar way, a 2D slice from a 3D grid of spheres appears as circles of different sizes, and a 3D slice of 4D space appears as spheres of different sizes in 3D space.
This explains the superiority of our 4D noise. A 3D slice of 4D noise has all the good properties that come from the dense, 4D packing. Inside the 3D slice the hyperspheres around each random number point appear as spheres of varying size. The excursion into 4D has given us a way to process spheres of different size while guaranteeing the uniform properties of the noise.