The packing problem is usually described as packing circles, spheres or hyperspheres. We are really interested only in the centres of the spheres but the geometry is the same. Mathematicians are still arguing over which packings are the densest in spaces of three or more dimensions. However, we don't need a proof that our packing is best. It is good enough.

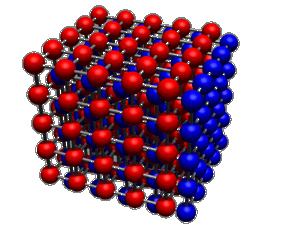
In four dimensions there is a particularly neat packing of hyperspheres. Imagine a  regular 3D grid of red spheres. The distance between adjacent spheres is 1.0. Then add a second grid as shown below.

The blue spheres each sit at the centre of eight red spheres. Now imagine that the blue spheres are moved in the fourth dimension by a distance of 0.5. This creates another 3D layer in the 4D space. If we repeat this construction we get a succession of layers each offset from the previous one. This produces a  4D grid that is really neatly packed. How do we know?

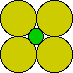
The second figure shows four yellow circles the same size, touching with a smaller, green circle inserted between them. You can do this in 3D and put a small sphere in the centre of eight. If you do it in 4D, the centre sphere will be the same size as the sixteen surrounding spheres. ( You can prove this using Pythagoras' theorem in 4D.) Our 4D packing is really tight because the distance from each blue sphere to the adjacent red spheres is the same as the separation between the adjacent red spheres. If we make the spheres bigger so the adjacent red spheres touch each other,  then they also touch the central blue sphere offset in the fourth dimension. Each hypersphere touches twenty four neighbours.