Question:
"Stand a cube on its corner. What is the shape of a horizontal cross-section taken at half the height of this object?"About 4% of us can reason about 3D space well enough to answer this question easily and with confidence. Most of us enter a state of panic when confronted by 3D problems. Yet it is possible to train yourself to think and visualize in 3D.
We take you through a series of exercises over one day that will start you thinking in 3D. Once you have the basic principles you can develop the skill independently.
Prerequisites: You should be familiar with some basic geometric ideas e.g: "two planes meet in a straight line." It is helpful if you know how to find distances with pythagoras' theorem, but this is used for only a few exercises and the course can be done without mathematics.
Background
In 1982, Bob Parslow discovered that a group of computer graphics students at Brunel university were unable to imagine clearly the shape of a cube.
It appears that about 96% of people cannot even find the corners of an imaginary cube standing on one corner. Bob described this phenomenon as "3D blindness" and after testing more than 4000 people, he has shown that even in such professional groups as engineering draftsmen, fewer than 30% have adequate skills at 3D visualization.
Since 1990, Bob and I have been giving a one day course in visualization skills. We have run this for undergraduate computer scientists, general public, at conferences in Lausanne, Melbourne, Hasselt and Hanover, at SIGGRAPH in 2001 and at GRAPHITE in 2003. We have demonstrated by these courses that the ability to imagine and reason about 3D shapes is a skill that can be learned.

After the course in Hanover we practise our skills on local sculpture.

Geoff demonstrating in Hanover 1998

Natalie after successfully constructing Super Nova Plexus
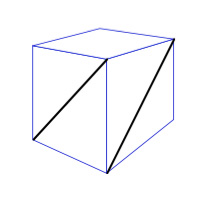
Unit Cube Diagonals
What is the distance between them?
It is not 1/sqrt(2)
What is the distance between them?
It is not 1/sqrt(2)